+++ author = “Elizar” categories = [“cryptography”] date = 2019-06-05T15:42:30Z excerpt = “Elliptic-curve Diffie–Hellman (ECDH) is an anonymous key agreement protocol that allows two parties, each having an elliptic-curve public–private key pair, to establish a shared secret over an insecure channel. " image = “https://res.cloudinary.com/dyd19kbsp/image/upload/v1648309490/gocrypto_g1cybv.jpg" tags = [“golang”, “security”, “cryptography”] title = “Generating ECDH Key Pair Using Go”

+++

What is ECDH?

Elliptic-curve Diffie–Hellman (ECDH) is an anonymous key agreement protocol that allows two parties, each having an elliptic-curve public–private key pair, to establish a shared secret over an insecure channel. This shared secret may be directly used as a key, or to derive another key. The key, or the derived key, can then be used to encrypt subsequent communications using a symmetric-key cipher. It is a variant of the Diffie–Hellman protocol using elliptic-curve cryptography.

Wiki

There’s an excellent article about Elliptic Curve Cryptography from Cloudflare’s blog. Check it out here.

Here’s the code

package main

import (
	"crypto/ecdsa"
	"crypto/elliptic"
	"crypto/rand"
	"fmt"

	"github.com/pkg/errors"
)

func main() {
	p, err := ecdsa.GenerateKey(elliptic.P256(), rand.Reader)
	if err != nil {
		panic(errors.Wrap(err, "Could not generate private key"))
	}

	privateKey := fmt.Sprintf("%x", p.D.Bytes())

	pBytes := elliptic.Marshal(p.PublicKey.Curve, p.PublicKey.X, p.PublicKey.Y)
	publicKey := fmt.Sprintf("%x", pBytes)

	fmt.Println("Private Key:", privateKey)
	fmt.Println("Public Key:", publicKey)
}

TRY IT!

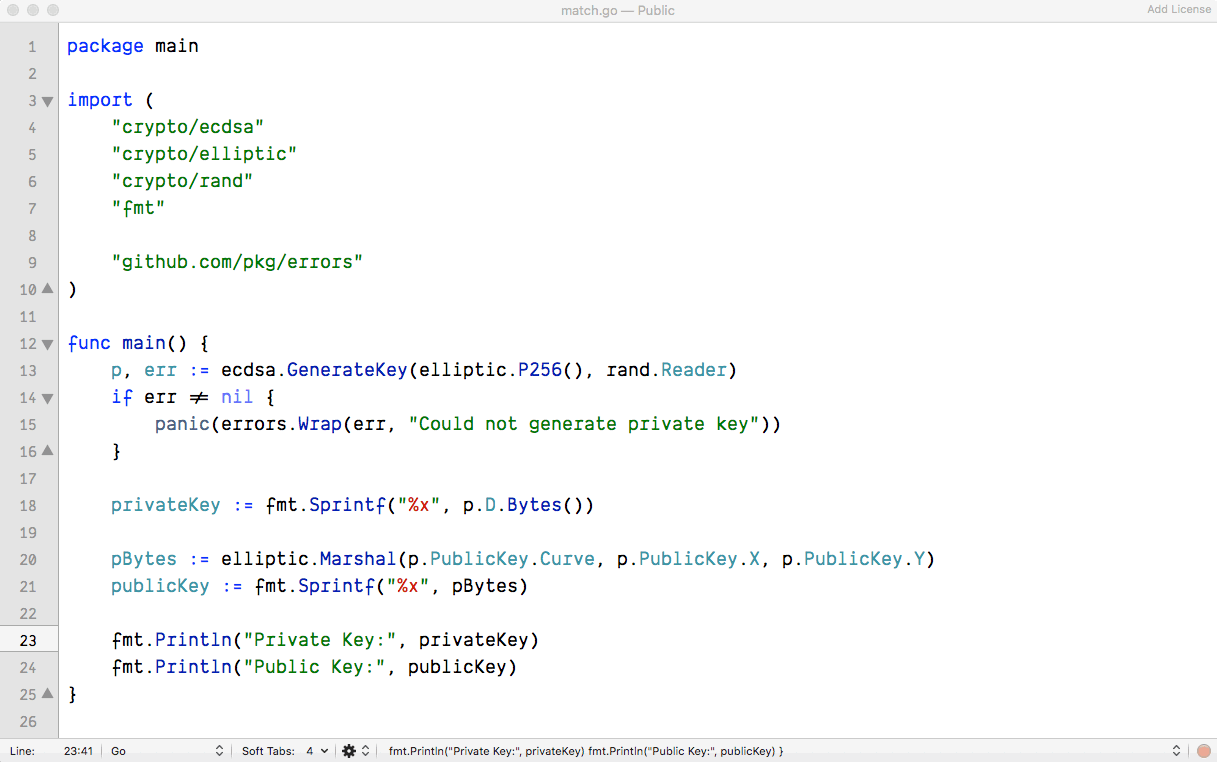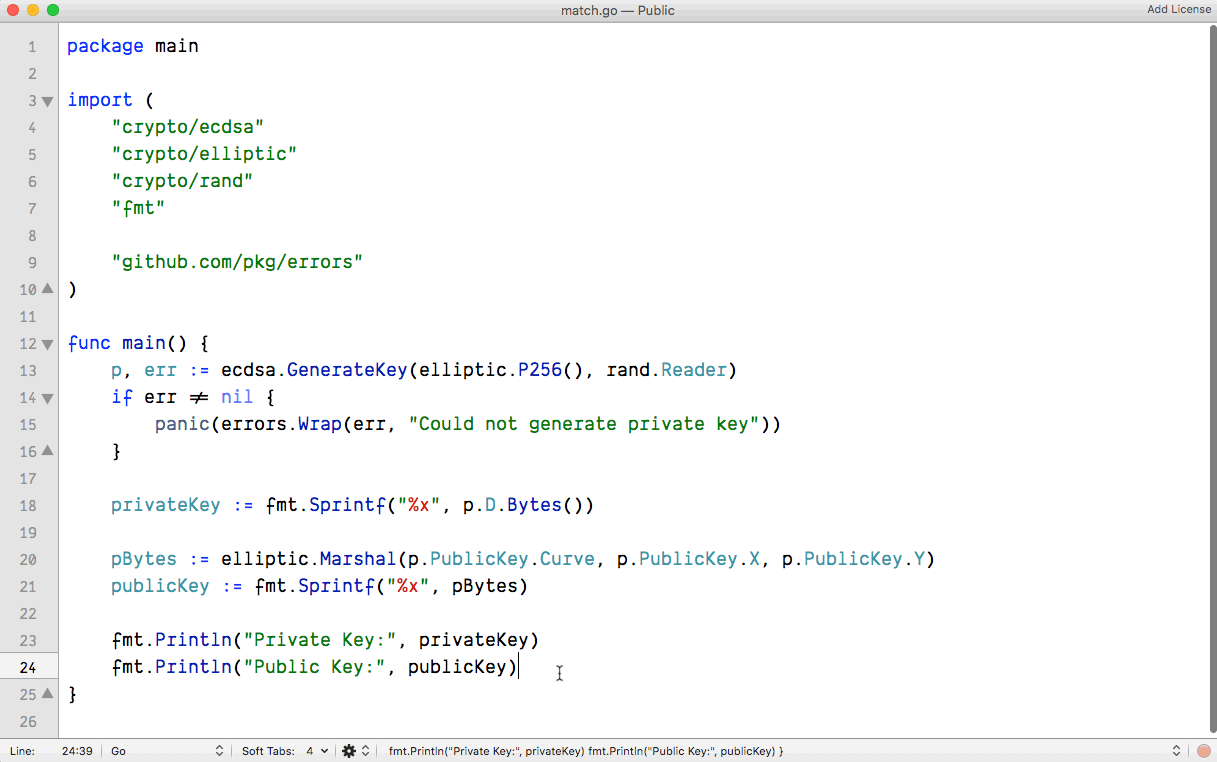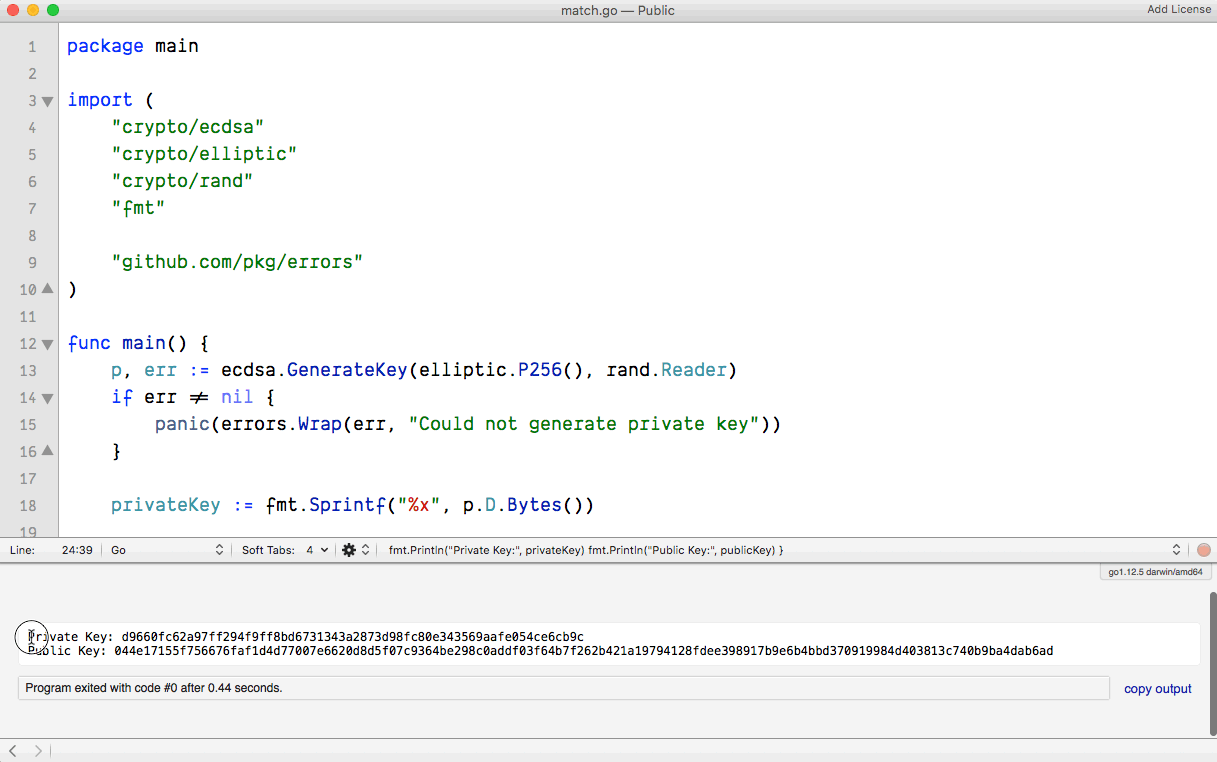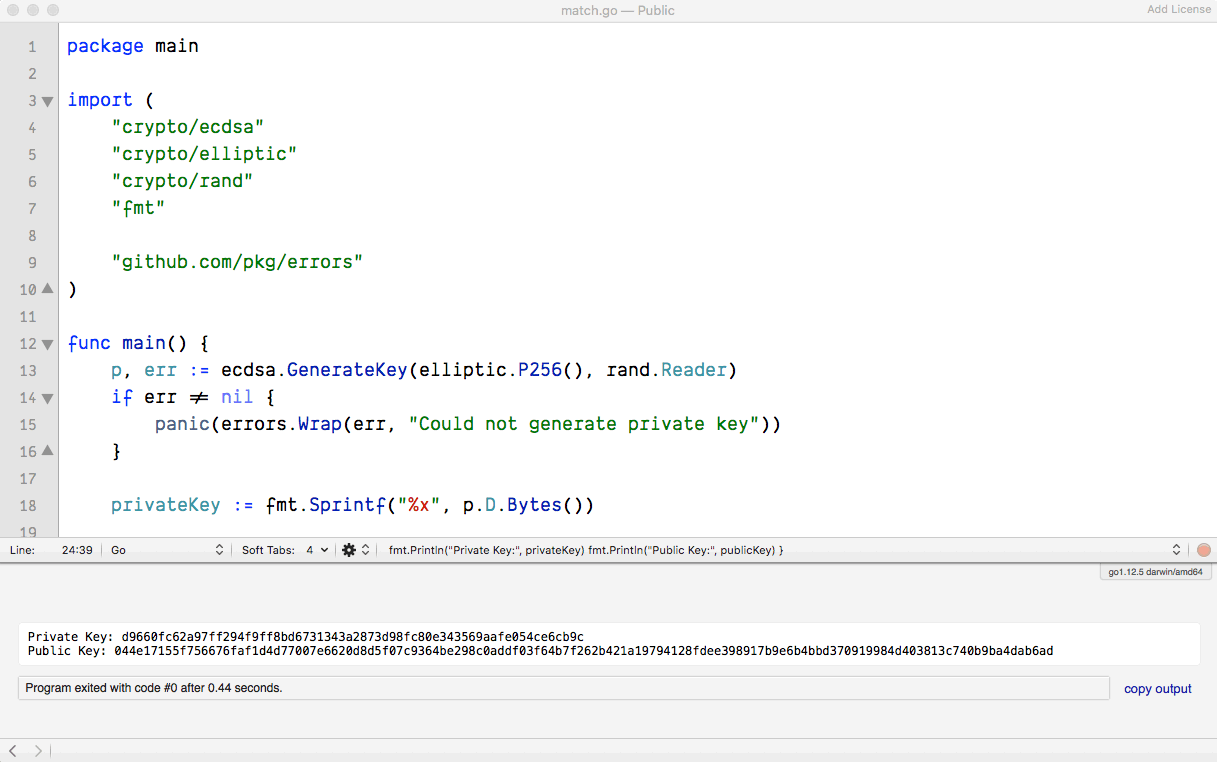
Running the ☝🏽 code will print something like the following:

Let’s break the code down

1. Private key generation.

p, err := ecdsa.GenerateKey(elliptic.P256(), rand.Reader)
if err != nil {
	panic(errors.Wrap(err, "Could not generate private key"))
}

We generate a private key using ecdsa.GenerateKey function. This function takes two arguments: elliptic.Curve and io.Reader and returns an instance of ecdsa.PrivateKey and an error if there is one.

For this example, I decided to use elliptic.P256() for the curve and rand.Reader as the random reader.

Note: elliptic.P256() is no longer safe to use btw, but I have my reasons which I will discuss on the later part of this series.

2. Extract both the private and public keys’ hex values.

privateKey := fmt.Sprintf("%x", p.D.Bytes())

The ecdsa.PrivateKey struct definition looks like this:

type PrivateKey struct {
	PublicKey
	D *big.Int
}

So to get the readable/string value of the private key, we have to get to D *big.Int instance first, and then call .Bytes() and store the result to a hex(base16) placeholder string "%x".

pBytes := elliptic.Marshal(p.PublicKey.Curve, p.PublicKey.X, p.PublicKey.Y)
publicKey := fmt.Sprintf("%x", pBytes)

The ecdsa.PublicKey struct definition looks like this:

type PublicKey struct {
	elliptic.Curve
	X, Y *big.Int
}

Getting the hex value of the public key needs a bit of extra work. For this example, we use elliptic.Marshal. There are, of course, other ways to do it, but this came to mind first while I was writing this article.

For the next part of this series, we will explore some good use cases for ECDH.

🖖🤓